Total Pageviews

Wednesday, February 6, 2019

CMOS Analog Design Basics: an example of transistor sizing when using the first time new techno ( e.g. 1um ) and we need NMOS transistor in saturation with ID=400uA and VGS bias is 1.5V

https://docs.google.com/document/d/1T7STY4RCtczVMoJTGfcYT43lXyCiwTUO5hNv8xqMIIc/edit?usp=sharing

Hi,


I just got into new 1um CMOS techno  so here is its transistors SPICE models:


You can download the SPICE model here: cmosedu_models.txt .
I would like to do sizing ( e.g. finding W/L ) of an NMOS transistor, so this transistor is in saturation
with ID = 400uA and biased with VGS=1.5V .
This is the transistor equation used for the sizing calculation:
  • μ is from Spice model :


  • Step 1: Cox is calculated using following formula:

where is a constant:
and 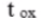( units are meters[m] ) is from Spice model of the transistor:


  • Here is a spreadsheet to calculate Cox:
N-mos ( techno data )


N-mos ( calculated data )

TOX[m]
UO [cm^^2/Vsec]

Cox[F/meter ^^2)
Cox[fF/micro meter ^^2)
2.00E-08
650

1.73E-03
1.73E+04
Or here is an Octave program that do the same Cox calculation:
#include <octave/oct.h>
syms ID min eox tox WdivL VGS VTH Cox min_times_Cox VDSsat R VDD
 
e0x = 3.9*8.854*power(10, -12) ;
 tox = 200*power(10,-10)        ; % units: m
 min = 650                      ;
 VDD = 5                        ;
 
 Cox = e0x/tox                  ;
 
 disp( "Cox =" ),  disp( Cox ), disp( "units: F/m2" ) ;
 
 Cox = (e0x/tox)*( power(10,15)/power(10,8) ) ;                
 
 disp( "or Cox =" ),  disp( Cox ), disp( "units: fF/micro-m2" ) ;
Result of the Octave  program run:
Cox =
 0.0017265
units: F/m2
or Cox =
   1.7265e+04
units: fF/micro-m2

  • Step 2:  Calculating  Cox * μ (units: F/Vsec)
    • Here is a spreadsheet to calculate Cox * μ :


N-mos ( techno data )


N-mos ( calculated data )


TOX[m]
UO [cm^^2/Vsec]

Cox[F/meter ^^2)
Cox[fF/micro meter ^^2)
Cox[F/micro meter ^^2)*UO [cm^^2/Vsec]=
Cox[F/micro meter ^^2)*UO [micro meter ^^2/Vsec]*10^^4[fF/micro meter ^^2]=
Cox[F/micro meter ^^2)*UO [micro meter ^^2/Vsec]*10^^4*10^^-15[F/micro meter ^^2]
2.00E-08
650

1.73E-03
1.73E+04
1.12224450E-04
Or here is an Octave program that do the same Cox * μ calculation:
#include <octave/oct.h>
 syms ID min eox tox WdivL VGS VTH Cox min_times_Cox VDSsat R VDD
 
 e0x = 3.9*8.854*power(10, -12) ;
 tox = 200*power(10,-10)        ; % units: m
 min = 650                      ;
 VDD = 5                        ;
 
 Cox = e0x/tox                  ;
 
 disp( "Cox =" ),  disp( Cox ), disp( "units: F/m2" ) ;
 
 Cox = (e0x/tox)*( power(10,15)/power(10,8) ) ;                
 
 disp( "or Cox =" ),  disp( Cox ), disp( "units: fF/micro-m2" ) ;
 
 min_times_Cox = min * Cox * power(10,4) * power(10,-15) ;
 disp ( "min * Cox =" ), disp( min_times_Cox ), disp( "units: F/Vsec" ) ;
Result of the Octave  program run:
Cox =
 0.0017265
units: F/m2
or Cox =
   1.7265e+04
units: fF/micro-m2
min * Cox =
   1.1222e-04
units: F/Vsec

  • Step 3:  Calculating  W/L

    • Summary:
      • Reminder, this is the equation we are using:
      • We know that we want:
        • ID = 400μA
      •  We know we will bias the transistor with :
        • VGS = 1.5V
      • From techno, meaning from SPICE model,  the value of Vth[V] is:
  • We already calculated  Cox * μ [F/Vsec] : 1.1222 * 10^^-4
=> W/L = 14.548 or approx. 15
Here is an Octave program that do the same W/L calculation:
#include <octave/oct.h>
 syms ID min eox tox WdivL VGS VTH Cox min_times_Cox VDSsat R VDD
 
 e0x = 3.9*8.854*power(10, -12) ;
 tox = 200*power(10,-10)        ; % units: m
 min = 650                      ;
 VDD = 5                        ;
 
 Cox = e0x/tox                  ;
 
 disp( "Cox =" ),  disp( Cox ), disp( "units: F/m2" ) ;
 
 Cox = (e0x/tox)*( power(10,15)/power(10,8) ) ;                
 
 disp( "or Cox =" ),  disp( Cox ), disp( "units: fF/micro-m2" ) ;
 
 min_times_Cox = min * Cox * power(10,4) * power(10,-15) ;
 disp ( "min * Cox =" ), disp( min_times_Cox ), disp( "units: F/Vsec" ) ;
f = -ID + (1/2)*min_times_Cox*(WdivL)*power((VGS-VTH),2)
% Substitute in values that are known
 newf = subs(f, [ID VGS VTH], [( 400*power(10, -6) ), 1.5, 0.8]);
% Solve the resulting symbolic expression for x
 result = solve(newf == 0, WdivL)
% And if you need a numeric (rather than symbolic) result
double(result)
Result of the Octave  program run:
Cox =
 0.0017265
units: F/m2
or Cox =
   1.7265e+04
units: fF/micro-m2
min * Cox =
   1.1222e-04
units: F/Vsec
f = (sym)

                           2
        7⋅WdivL⋅(VGS - VTH)
 -ID + ────────────────────
               124750

result = (sym)

 4990
  ────
  343

ans =  14.548

  • Step 4:  Verifying that when we have an NMOS ( in the techno used ) with  W/L = 15 and
  • we bias it with VGS=1.5V and alim. for this techno is VDD=5V,
                  • then the transistor  should be in saturation with ID = 400μA
    • For this verification I will use LTSpice simulation of following schematic:
Here is how I calculated R1 = 10.77K in this schematic:

Step 4.1: to calculate R1 we would need VDSsat because R1= (VDD -VDSsat)/IDS

  • R1= (5V -VDSsat)/400μA
  • A friendly reminder: we are still using the same equation:
      • We know that we want:
        • ID = 400μA
  • We already calculated  Cox * μ [F/Vsec] : 1.1222 * 10^^-4
  • We already calculated ( under assumption that VGS = 1.5 V and
knowing from the techno, meaning from SPICE model,
that  the value of Vth[V] is:
=> W/L = approx. 15


Note*: We expect VDSsat minimum to be VGS - Vth = 1.5 - 0.8 = 0.7V  
Here is a Octave program to calculate VDSsat:
#include <octave/oct.h>
 syms ID min eox tox WdivL VGS VTH Cox min_times_Cox VDSsat R VDD
 
 e0x = 3.9*8.854*power(10, -12) ;
 tox = 200*power(10,-10)        ; % units: m
 min = 650                      ;
 VDD = 5                        ;
 
 Cox = e0x/tox                  ;
 
 disp( "Cox =" ),  disp( Cox ), disp( "units: F/m2" ) ;
 
 Cox = (e0x/tox)*( power(10,15)/power(10,8) ) ;                
 
 disp( "or Cox =" ),  disp( Cox ), disp( "units: fF/micro-m2" ) ;
 
 min_times_Cox = min * Cox * power(10,4) * power(10,-15) ;
 disp ( "min * Cox =" ), disp( min_times_Cox ), disp( "units: F/Vsec" ) ;
f = -ID + (1/2)*min_times_Cox*(WdivL)*power((VGS-VTH),2)
% Substitute in values that are known
 newf = subs(f, [ID VGS VTH], [( 400*power(10, -6) ), 1.5, 0.8]);
% Solve the resulting symbolic expression for x
 result = solve(newf == 0, WdivL)
% And if you need a numeric (rather than symbolic) result
double(result)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f = -ID + (1/2)*min_times_Cox*(WdivL)*power(VDSsat,2)
% Substitute in values that are known
 newf = subs(f, [ID WdivL] , [( 400*power(10, -6) ), 15 ]);
 
 % Solve the resulting symbolic expression for x
 result = solve(newf == 0,VDSsat)
 
 % And if you need a numeric (rather than symbolic) result
double(result)
Result of the Octave  program run:
Cox =
 0.0017265
units: F/m2
or Cox =
   1.7265e+04
units: fF/micro-m2
min * Cox =
   1.1222e-04
units: F/Vsec
f = (sym)

                           2
        7⋅WdivL⋅(VGS - VTH)
 -ID + ────────────────────
               124750

result = (sym)

 4990
  ────
  343

ans =  14.548
f = (sym)

                2
       7⋅VDSsat ⋅WdivL
  -ID + ───────────────
             124750

result = (sym 2×1 matrix)

  ⎡-√20958 ⎤
  ⎢────────⎥
  ⎢ 210   ⎥
  ⎢       ⎥
  ⎢ √20958 ⎥
  ⎢ ────── ⎥
  ⎣ 210   ⎦

ans =

  -0.68938
   0.68938
Source code of Octave program is here: octave_program

Step 4.2:

  • A friendly reminder from previous step: R1= (5V -VDSsat)/400μA
=>  R1 = (5V -0.68938)/400μA
=> R1 = 1.0777e+04 = approx. 10.78KΩ
LTspice simulation showed: IDS = 354 μA  (expected 400 μA ) and VDSsat= 1.18V ( expected result:  689mV )
Name:          m1
Model:        n_1u
Id:          3.54e-04
Vgs:         1.50e+00
Vds:         1.18e+00
Vbs:         0.00e+00
Vth:         8.39e-01
Vdsat:       5.59e-01
Finally, by fine adjusting  of W/L from 15 to 17, LTspice simulation showed: IDS = approx.  398 μA (expected 400 μA ) and VDSsat= approx. 711mV ( expected result:  689mV )


Name:          m1
Model:        n_1u
Id:          3.98e-04
Vgs:         1.50e+00
Vds:         7.11e-01
Vbs:         0.00e+00
Vth:         8.39e-01
Vdsat:       5.60e-01

 © 2011 ASIC Stoic. All rights reserved.

Posted by at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)